Settling slurry flow

Settling slurry flow

In settling slurry, larger and denser particles settle out of the liquid and form a bed at the bottom of the pipe. If the size of the transported particles is in the range of the medium sand range (say between 200 µm and 800 µm), the flow exhibits heterogeneous behavior, with smaller values of flow velocity producing non-uniformity in distributions of both solids concentration and solids velocity, and increases in hydraulic gradient beyond that given by i_mh.

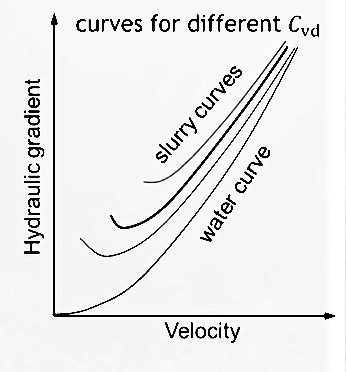
In heterogeneous flow, a pipe characteristic curve for slurry flow of constant delivered concentration exhibits the minimum point. The change in the trend of the hydraulic gradient with the decreasing velocity approaching the velocity at which the gradient is minimal is associated with increasing stratification of the flow and the establishment of a granular bed at the bottom of the pipe. The velocity at the minimum is usually close to the deposition-limit velocity. The presence of the minimum on the pipe curve has consequences for the interaction with the pump characteristic curve and hence for the stability of the operation of the pump-pipeline system. Note that if the flow velocity increases, then the pipe curve tends to follow the curve of the carrying liquid, indicating that the concentration of solids to the total pressure gradient decreases with the increasing velocity. This is due to the decreasing proportion of contact-load particles with the increase in the velocity of the heterogeneous flow.

In the 1950s, Durand and Gilbert obtained an equation by data correlation technique, which produced gradient-velocity curves with a minimum. The equation refers to friction loses in horizontal pipe flow.

Here, i_m is the frictional hydraulic gradient of the mixture, i_w is the gradient flow for an equal flow of water alone, C_vd (delivered concentration) is the ratio of volumetric flow rates of solids and mixture, and C_vi (in-situ concentration) is the ratio of volume of solids and the total volume of mixture.

Although Durand’s equation has been widely used for many settling slurries, it shows poor agreement with the data. Newitt et al. (1955) divided particular slurry flows into three types: homogenous or pseudo-homogenous flow, heterogeneous flow, and stratified flow. For stratified flow, the concept of mechanical sliding friction between moving solids and pipes was utilized. Assuming an essentially two-dimensional fully-stratified flow with a negligible difference between delivered and in-situ concentration, it was suggested that i_m - i_w should be directly proportional to (S_m - 1), where S_m is the relative density of the mixture. i.e.

From the data, Newitt et al. evaluated B as about 0.8 and proposed that the above equation applies provided that V­m ≤ 17 v_t, where v_t is the terminal settling velocity of the solid and V_m is the mean velocity. It can be seen that the above equation for fully-stratified flow reflects a domain in which variations in particle size or fall velocity do not affect the pressure gradient.