What Is Friction.
Friction can be defined as a force which opposes the relative motion between two elements in contact. Friction converts the kinetic energy of the moving bodies into heat energy causing useful work loss.
Friction in fluids occur due to a the friction between the layers of fluids moving relative to each other. The friction in fluids is dependent on a property called viscosity. This is the resistance offered to flow or deformation by a fluid.
Fluid Friction In Pipes
Pressure drops or head loss can be experienced in pipes carrying fluids due to the frictional forces between the boundary layer(outer layer) of the moving fluid and the internal surface of the pipe combined with the viscosity. The extent of head loss is dependent on some factors in the fluid, some of these factors are:
Re = Vavg × ρ × D / μ
Other factors which influence the head loss from friction in a pipe are: viscosity, temperature, pipe diameter, flow velocity etc.
When designing piping systems, identifying the head loss due to friction is of paramount importance because it makes up the majority of losses in pipe flow. To that end, several models have been developed to try and approximate the operation of these pipes under various condition so that the losses from friction can be easily approximated and accounted for. Here are some of them:
Moody Friction Model
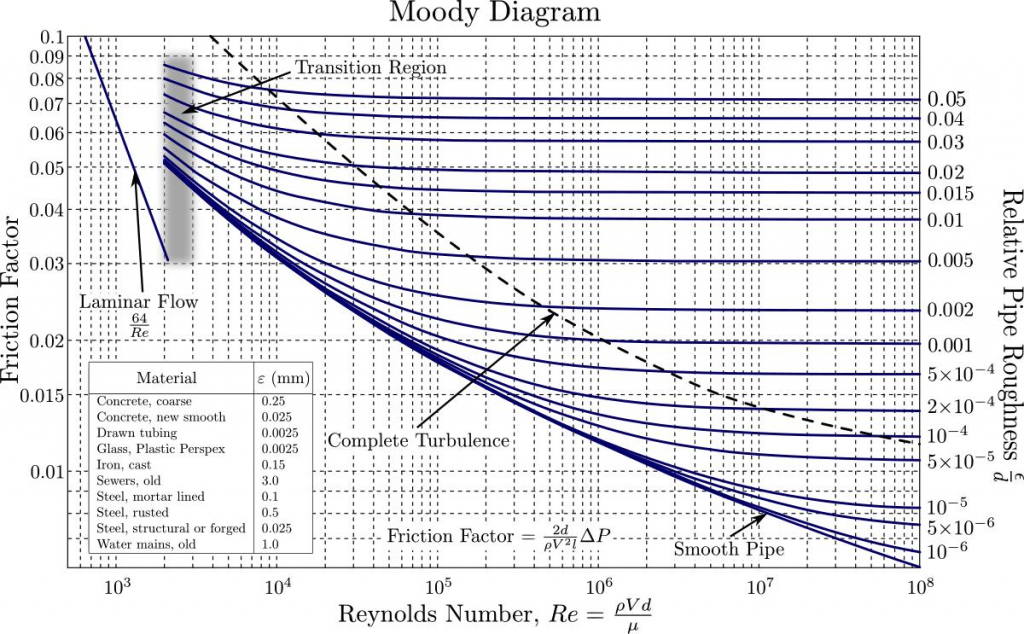
The Moody Diagram is a chart plotted by engineer Lewis F. Moody in the early 20th century. Through experiments, he found out that the type of flow in pipes could be described by four dimensionless parameters: Reynolds number, pressure loss coefficient of the pipe, diameter ratio and the relative roughness of the pipe). He then represented this on a graph by plotting the Reynold number, relative roughness and Darcy - Weisbach friction factor against each other.
Formula
Applications
The Moody chart is used extensively in calculating head loss and pressure drops in pipes in tandem with the Darcy-Weisbach equation. The friction factor for different flow regimes (laminar, turbulent and transitional) can be gotten from the Moody diagram. which is then substituted into the Darcy-Weisbach equation. To find the head loss.
Example 1
Water at 35oC is flowing through a steel pipe of diameter 100mm at 3m/s. Calculate the Moody friction factor for:
Solution
From the values given, we have: temperature = 35C, pipe internal diameter = 0.1m, velocity = 3m/s, density = 994.1 kg/m 3 , kinematic viscosity = 0.000720 kg/m sec (From standard steam tables). With these values, we find the Reynolds number with (1):
Re = Vavg × ρ × D / μ = 3 * 994.1 * 0.1 / 0.000720 = 414208. approx 4.14× 105
We then find the absolute roughness by dividing the relative roughness(ϵ) by the pipe diameter(D). For a smooth steel pipe we have relative roughness = 0.000061m. For a corroded pipe we have relative roughness = 0.004m(The American Iron & Steel Institute Committee for Steel Pipe Producers)
Calculating the absolute roughness:
For the smooth pipe = 0.000061/0.1 = 0.00061
For the corroded pipe = 0.004/0.1 = 0.04
Consulting the Moody chart, we have Darcy friction factors.
For the smooth pipe: 0.018
For the corroded pipe: 0.029
Advantages
Disadvantages
Hazen - Williams Friction Model
The Hazen -Williams friction model was developed for use in water pipe systems, although in recent times, it has found use in refined petroleum pipelines. It was initially developed as an alternative to the Darcy - Weisbach equation because the Darcy friction factor was difficult to calculate for turbulent flows in the past.
Formula
The Hazen-Williams equation calculates the head loss or pressure drop in water pipelines when the pipe diameter and flow rate is given, taking into account a factor C which is dependent on the internal smoothness of the pipe. The formula used to calculate the
head loss is:
Where L= Length of pipe(m), Q = Flow rate(m3/s), D =Pipe inside diameter(m), C = Hazen - Williams C factor.
*The coefficient of smoothness C is a factor that increases with increasing smoothness of the pipe.
Applications
The Hazen -Williams equation is primarily used in the design of water distribution systems such as irrigation pipelines, water sprinklers and fire stations. It is also applied in refined petroleum pipelines.
Example 1
For the conditions given in example 1, find the head loss due to friction for both the smooth and corroded pipe using the Hazen - Williams equation.
Solution
In example I, we had velocity(v) = 3m/s, equivalent length = 500m, pipe internal diameter = 0.1m. Q = velocity *area of pipe = 0.024m3 /s
To find the head loss due to friction, we need the Coefficient of Smoothness C which is 140 for smooth steel pipe and 100 for the corroded steel pipe.(The American Iron & Steel Institute Committee for Steel Pipe Producers)
So, substituting the values into (2), we have:
Head loss in the smooth pipe:
hL = 10.67 * 500 * (0.024)1.87 ÷ (1401.852 * 0.14.87 ) = 40.54m
Head loss in the corroded steel pipe:
hL = 10.67 * 500 * (0.024)1.87 ÷ (1001.852 * 0.14.87 ) = 75.6m
Advantages
Disadvantages
Darcy - Weisbach Friction Model
The Darcy-Weisbach equation is the most commonly used formula in determining the head loss in pipes. The Darcy - Weisbach equation is an empirical equation that relates the head loss or pressure loss due to friction in a pipe to the average velocity of the fluid.
Formula
The head loss formula for the Darcy Weisbach equation utilizes a special friction factor fd known as the Darcy Friction Factor, the equivalent length and pipe diameter in order to relate the head loss to friction to the velocity head. It is expressed as:
hL = fD × (L/D) × V2/2g……..(4)
Where fd =Darcy friction factor, L=Equivalent length of pipe, D = Diameter of pipe, V = Velocity of the fluid, g = acceleration due to gravity
The Darcy friction factor can be gotten by a number of methods. The easiest way is to read it from the Moody Chart. It can also be gotten by solving the respective equations.
For Laminar flow: fd = 64/Re
For turbulent flow, we can solve the Colebrook-White equation for fd
Where e = Absolute roughness(m), D = Pipe internal diameter, Re =Reynolds number.
*The Darcy Weisbach equation assumes the flow is unaffected by the pipes roughness when the flow is laminar.
Applications
The Darcy-Weisbach is widely viewed as the most accurate equation used in calculating the friction loss for incompressible Newtonian fluid flow in pipes. It is applied in designing piping systems for various fluids and even in some low speed gas flows over short distances provided there aren’t any major changes in density.
Other equations like the Hazen-Williams equation were used before in determining the head loss because of the difficulty encountered in obtaining the friction factor fd. But with the advent of new and faster computing methods the Darcy-Weisbach formula has emerged as the preferred equation for calculating the head loss in incompressible fluid flow in pipes.
Example 3
For the conditions given in example 1, calculate the head loss due to friction in the pipe using the Darcy - Weisbach equation.
Solution
We have velocity(v) = 3m/s, acceleration due to gravity(g) = 9.81m/s2 , equivalent
length = 500m, pipe ID = 0.1m, Darcy friction factor = 0.018 for smooth steel pipe,
0.04 for corroded pipe(example 1)
Substituting these values into (4) to find the head loss, we have:
For the smooth pipe, we have
hL = 0.018 * (500/0.1) * (32 /2 * 9.81) = 41.2m
For the corroded pipe, we have
hL = 0.04 * (500/0.1) * (32 /2 *9.81) = 91.73m
Advantages
Disadvantages
Shell-MIT Friction Model.
This model was developed by the petroleum company Shell in conjunction with MIT. It was primary developed for use in oil pipeline engineering. The pipelines were used for transporting heavy crude oils that undergo heating to reduce their viscosity and enhance pipe flow..
Formula
The Shell-MIT formula uses a modified Reynolds number in its calculations. This
modified Reynolds number is gotten by diving the Reynolds number by 772.
Rem = Re/ 772.……(5)
Where Rem =Modified Reynolds number, Re= Reynolds number
The friction factor is then calculated with the modified Reynold’s number:
f = 0.00207 + Rem ( For laminar flow)
f = 0.0018 +0.00662(1/Rem)0.355 (For turbulent flow)
*This is different from the Darcy - Weisbach friction factor.
The friction factor is then used to calculate the pressure drop in the pipeline using this
formula.
Pm = 6.2191× 1010 (f ×Sg×Q2 ) / D5 ……..(6)
Where Pm = Frictional pressure drop (kPa/km), f = friction factor, Sg =Specific
gravity of the liquid, Q = flow rate(m3/hr), D = pipe internal diameter(mm).
Application
The Shell-MIT equation is used specifically in the petroleum industry to calculate the pressure drop in heavy crude oil and heated pipelines.
Advantages
Disadvantages
Other equations like the Miller and Aude equations are used in the oil industry for calculating the pressure drop in crude oil pipelines. They have been replaced by the Shell-MIT equation due to certain restrictions and difficulties encountered when using
them.
Conclusion
Comparing the values from the Hazen -Williams and the Darcy Weisbach factor.
From the results gotten, we can see that:
1. There is clear agreement between the two methods for a smooth (clean) pipe with
just a little variation in the values gotten.
2. As the pipe roughness increases, the variation between the two methods also
increases. This increase is due to the discrepancies between the various
experimental methods used to derive the relative toughness and the smoothness
coefficient C for the rough pipes.
In conclusion, the Darcy-Weisbach model is the best model to use by default in fluid
pipe flow.
It takes into consideration factors such as density and kinematic viscosity which have
a pronounced effect on the Reynolds number which can in turn impact the losses in
the pipe flow. It is also retains it’s validity over a wide range of temperatures for
Newtonian fluids.
With advances in computation, the Darcy friction factor has also become easier to
calculate which makes using the Darcy- Weisbach equation easier.
References
We aim to provide responsive service. Please contact us and
we will do our best to address your query: